El Casino de Monte Carlo y las radiaciones

Hay que reconocer que Stanislaw Ulam y John von Neumann tuvieron su momento de inspiración al bautizarlo Método Monte Carlo. Y no era otra cosa que un método de resolución aproximada del transporte de partículas mediante el uso de números aleatorios. En realidad el nombre fue sugerencia de su colega Nicholas Metropolis que relacionó el aspecto aleatorio del método con el hecho de que Ulam tuviera un tío que solía pedir dinero a la familia porque «tenía que ir al casino de Monte Carlo», en el Principado de Mónaco. El nombre tuvo tanta aceptación que se generalizó a todo método de aproximación basado en el uso de números aleatorios, no sólo a su aplicación al transporte de partículas. Pero muchos diréis ¿y quiénes son esos personajes? Eran físicos estadounidenses de origen europeo que trabajaron conjuntamente en el Proyecto Manhattan durante la Segunda Guerra Mundial y en los años posteriores.

Pero estrictamente hablando ellos no fueron los inventores del método. Quizás la primera documentación sobre el uso de un muestreo aleatorio para encontrar una solución a un problema es la del naturalista francés Georges Louis Leclerc, conde de Buffon.

Extracto del capítulo 11 de «Érase una vez… los inventos». Se habla del conde de Buffon y el muestreo aleatorio a partir del minuto 4:11

En 1777 describió el siguiente experimento: una aguja de longitud L se lanza aleatoriamente sobre una hoja de papel rayada con líneas rectas separadas una distancia d (con d mayor que L). ¿Cuál es la probabilidad P de que una aguja caiga cruzando una de las líneas? Leclerc realizó el experimento lanzando la aguja multitud de veces para determinar P. También llevó a cabo el análisis matemático para encontrar que dicha probabilidad estaba relacionada con la longitud de la aguja L y la separación entre líneas d a través del número π. Es por tanto una forma de determinar el número π mediante el método Monte Carlo. Pero si os disponéis a realizar la prueba, armaos de paciencia porque hay que tirar muchas agujas para que el resultado empiece a parecerse al valor real.

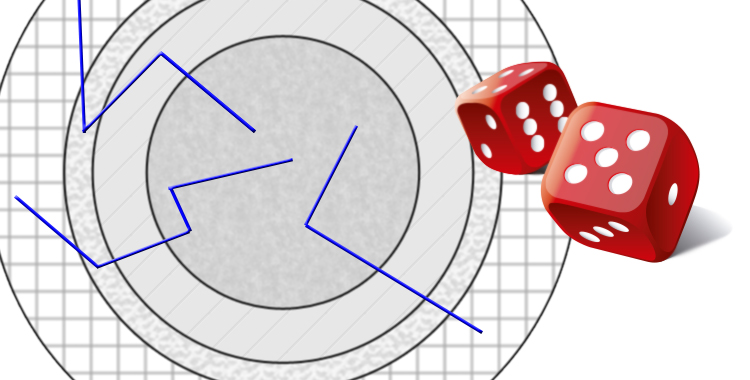
Simulación por ordenador del experimento de Leclerc con 60 agujas de longitud L lanzadas sobre una hoja con 5 líneas separadas una distancia d tal que L/d=3/4.  La probabilidad de que una de las agujas cruce alguna de las líneas es: P=2L/πd
Si en esta simulación 29 agujas cruzan alguna línea, ¿cuál es la estimación del valor de π ? No os robaré el placer de calcularlo por vosotros mismos.

Lord Kelvin también usó el muestreo aleatorio para evaluar unas integrales de la teoría cinética de los gases. En una publicación de 1901¹, describía cómo había numerado trozos de papel que posteriormente extraía de un cuenco. Pero él mismo ponía de manifiesto lo poco que le convencía el método, ante la dificultad de mezclar adecuadamente los trozos o incluso cómo la electricidad estática provocaba que en ocasiones sacara varios trozos de una vez.

Existen otros ejemplos documentados sobre el uso del muestreo aleatorio antes de los años cuarenta, pero podemos considerar a Ulam y von Neumann los creadores del método Monte Carlo como lo conocemos hoy día, al realizar una descripción completa del método e incluirle un ingrediente que le confirió un potencial excepcional: la utilización de computadoras electrónicas.

Al terminar la Segunda Guerra Mundial, en la Universidad de Pensilvania se construyó la primera computadora electrónica, ENIAC, con más de 17.000 válvulas de vacío y otras tantas resistencias, diodos y condensadores. Su objetivo inicial era realizar cálculos balísticos para el ejército estadounidense, que hasta ese momento eran efectuados por un ingente grupo de personas con calculadoras convencionales de la época. John von Neumann, que ejercía de consultor tanto para el ejército como para el Laboratorio Nacional de Los Alamos, implicado en el Proyecto Manhattan, convenció al ejército para ceder el poder de cálculo de ENIAC para comprobar modelos de reacciones nucleares.

¿En qué consistían esos cálculos? Un ejemplo es la difusión de neutrones en un material fisionable. Los modelos iniciales consideraban una esfera de material fisionable rodeada de un material de alta densidad. Se asumía una distribución inicial de neutrones con diferentes velocidades. La idea era seguir el movimiento de un gran número de neutrones individuales que pueden sufrir dispersiones, absorciones, fisionar núcleos y escapar de la esfera. En primer lugar se toma un neutrón en concreto con una posición y velocidad dadas. Entonces hay que decidir en qué punto va a sufrir una colisión y de qué naturaleza será. Si se ha determinado que sea una fisión por ejemplo, debe decidirse el número de neutrones que emergerán, los cuales deben ser seguidos como el que provocó la fisión. En cambio, si la colisión es una dispersión, debe determinarse su nueva velocidad. Una vez seguido el primer neutrón y todos los que produjera por fisiones hasta que sean absorbidos o abandonen la geometría, tendríamos que se ha concluido la “historia” de ese neutrón. Como resultado, el medio ha sufrido una cierta perturbación que habremos calculado. Esa perturbación puede ser, por ejemplo, la energía cedida al medio por los neutrones. Este mismo proceso se repite tantas veces como sea necesario hasta apreciar que el promedio de esa perturbación tiende a un valor estable.

Pero, ¿cómo se decide qué evento sufre cada neutrón y cuál será la longitud recorrida entre eventos consecutivos? Aquí es donde entran en juego los números aleatorios. Como sí conocemos las funciones de probabilidad de ocurrencia de los diferentes eventos posibles, tan sólo se trata de muestrear aleatoriamente dichas funciones cada vez que se requiera determinar la longitud de una trayectoria, qué evento va a tener lugar y qué características van a tener los productos de dicho evento, si los hay. De la simulación de numerosas historias obtenemos un resultado promedio. Pero dicho resultado va cambiando conforme aumenta el número de historias. ¿Cómo podemos saber lo cerca que estamos del valor que estamos buscando? Para ello nos ayudamos de la varianza de los mismos. Cuanto menor sea esa varianza, más cerca del valor buscado nos encontraremos. Como regla general podemos decir que la varianza es inversamente proporcional al número de historias simuladas. Si queremos tener un resultado muy preciso, es necesario simular un alto número de historias.

Antes de disponer de ENIAC se realizaban dichas simulaciones con calculadoras mecánicas. Es fácil intuir que se requería tanto tiempo para alcanzar resultados fiables que su abordaje era inviable. Enrico Fermi, que ya había hecho incursiones en este mundo de la estimación estadística en los años treinta, sin publicar sus métodos, diseñó un artilugio que llamó FERMIAC. Consistía en una serie de ruedas que se ajustaban según el material en el que se encontrara el neutrón y permitía dibujar trayectorias sobre un gráfico bidimensional. Este dispositivo se estuvo utilizando durante un período de tiempo en el que ENIAC no estuvo operativo debido a un traslado de centro de operaciones.

Stanislaw Ulam con el FERMIAC

Ejemplo de uso del FERMIAC sobre un gráfico bidimensional. El dispositivo puede verse en el Bradbury Science Museum en Los Alamos

En los primeros años tras la difusión del método Monte Carlo asistido por computadoras podría decirse que tuvo una aplicación limitada. Eran muy pocos los científicos que disponían de dicho tipo de computadoras y su programación era muy compleja. En 1954, Hayward y Hubbell simularon la trayectoria de 67 fotones utilizando calculadoras mecánicas y una lista de números aleatorios. En la década de los cincuenta había una cierta insistencia en aplicar el método en la resolución de cualquier de tipo de problema, resultando ser en muchos casos un método menos eficiente que otras herramientas de análisis numérico, lo que contribuía a su desacreditación ante la comunidad científica.

Fue a partir de los años sesenta cuando se empezó a tener en mejor consideración por varias razones. Se consiguió un mejor reconocimiento de aquellos problemas en los que era la mejor ―y en algunos casos la única― técnica disponible. También hubo un continuo progreso en la construcción de las computadoras electrónicas que las hacía cada vez más asequibles y rápidas en sus cálculos.

La programación de las simulaciones también se facilitó considerablemente con el desarrollo de códigos Monte Carlo que permiten la simulación del transporte de radiación con la mera introducción de unos parámetros que definen el problema en cuestión. Los usuarios de estos códigos no tienen que preocuparse de aspectos como la generación de números aleatorios ni de la definición de funciones de distribución de probabilidad de eventos. Entre esos códigos podemos encontrar MCNP (desarrollado por el propio laboratorio de Los Alamos), EGS4, Geant4, Fluka, ¡e incluso tenemos uno español! PENELOPE desarrollado en la Universidad de Barcelona, el cual goza de un gran prestigio sobre todo en el ámbito de la física médica. Aunque inicialmente había un gran interés por el transporte de neutrones, ya podemos encontrar que esos códigos pueden utilizarse para el transporte de otros tipos de partículas como fotones, electrones, etc.

Actualmente los métodos Monte Carlo son ampliamente utilizados en el estudio de problemas tan diversos como evaluación de integrales en matemáticas, crecimiento de bosques y estudios de contaminación en ingeniería ambiental, análisis de mercado en economía, y un largo etcétera.

Por supuesto os podéis imaginar el impacto que ha tenido el desarrollo de códigos de simulación del transporte de radiación en el uso médico de las radiaciones ionizantes. Pero su aplicación en la medicina no sólo se centra en el estudio de la interacción de la radiación con materia. En procesos en los que podemos encontrar una alta variabilidad, como es el caso de la respuesta de los tejidos y tumores en los tratamientos radioterápicos, obtener resultados a partir de los ensayos con pacientes requiere de un esfuerzo desmesurado en muchos casos. Es aquí donde la simulación Monte Carlo aporta una información muy valiosa que pueda servir de apoyo en el avance científico².

Como curiosidad, en 1971 Luke Rhinehart publicó la novela «El hombre de los dados»³. El método Monte Carlo es llevado a su extremo por un psiquiatra que decide volverse un “hombre aleatorio” tomando todas sus decisiones a partir de los resultados del lanzamiento de un par de dados.

¹ Lord Kelvin, «I. Nineteenth century clouds over the dynamical theory of heat and light,» The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 2 (7), 1-40 (1901).

² D. Guirado Llorente, Variabilidad en radiobiología. Universidad de Granada, Granada, 2012.

³ L. Rhinehart, El Hombre de los dados. Editorial Destino, Madrid, 2003.